EI hombre es un animal limitado. Y entre sus muchos defectos hay uno que ha jugado un papel fundamental en la historia de los números: no posee percepción directa e inmediata de grupos de objetos mayores de 4 unidades. Es decir, sin aprendizaje previo, sólo puede reconocer de un golpe cuándo un grupo esta formado por 1, 2, 3 o 4 individuos. A partir de ahí, se ve obligado a contar. Y es precisamente eso lo que viene haciendo desde tiempos inmemoriales con el fin de adaptarse al medio, aprovechar las oportunidades del entorno, evitar amenazas y transmitir bienes a otros miembros de la especie.

Todavía es un misterio la determinación del momento exacto en el que el ser humano aprendió a contar. Pero lo que sí está claro es que, para ello, debió de servirse de ciertas herramientas de apoyo. Incluso hoy en día, algunos grupos étnicos de Oceanía, América, Asia y África emplean un lenguaje matemático que sólo incluye las palabras uno, dos y muchos. Pero eso no quiere decir que sean incapaces de ordenar las cantidades. Algunos utilizan sistemas de muescas en madera, otros apilan piedrecitas y otros recurren a partes de su cuerpo como los dedos, los ojos o las orejas para realizar sus cuentas.

Algo así debieron hacer los primeros seres humanos que se embarcaron en la aventura de los números. Primero, utilizando las múltiples fuentes de referencia que suministra la naturaleza (las alas de un pájaro para el concepto de dos, las patas de un perro para el de cuatro...) y, más adelante, usando su propio cuerpo. Por eso la mayor parte de los sistemas de numeración de hoy en día son de base 10, número de dedos de las manos. Hay algunas excepciones, como los mayas, los aztecas y los celtas, que contaban con sistemas de base 20, porque utilizaban los dedos de los pies y de las manos. Todavía hoy perdura la huella de este modo de numeración. Por ejemplo, en francés, 80 se dice cuatro veintes. Por su parte, los sumerios y babilonios sumaban en complicados grupos de 60. De ellos hemos heredado hoy la división del tiempo en horas de 60 minutos y minutos de 60 segundos, y la partición del círculo en 360 grados.

Hace 6.000 años
¿Pero cuándo se dio el paso de la contabilidad manual a la escritura de los números? Los últimos datos históricos parecen evidenciar que tal prodigio sucedió en Elam, tierra perteneciente al actual Irán, 4.000 años antes de Cristo. Allí se creó un rudimentario sistema de símbolos cuneiformes para representar algunos números que luego fue adoptado por los sumerios de la Baja Mesopotamia. A este último pueblo le corresponde el honor de haber creado las cifras más antiguas de la historia, antes incluso de la aparición de la escritura.

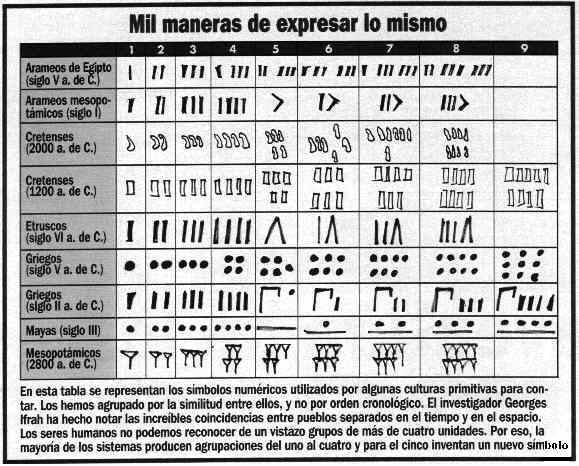A partir de la elección de determinados símbolos para representar las cantidades, la historia de los números no es mas que un fascinante proceso de perfeccionamiento. En la mayoría de los sistemas de numeración de las civilizaciones mesopotámica y egipcia se seguía un criterio de agrupamiento de los símbolos para construir estructuras fácilmente identificables a primera vista. Pero cuando los números son realmente grandes, este truco tampoco es eficaz.

El problema de los grandes
Algunos escribas egipcios inventaron un símbolo para la decena similar a una U invertida. Así, cuando se trataba de escribir 11, lo que en realidad se hacía era simbolizar 10 + 1 o 1 + 10. Con otro símbolo distinto representaban un centenar y otro para el millar.
Así surgió una numeraci6n egipcia que sirvió de base a las posteriores formas de contar griega y romana, basadas en la repetición de símbolos y la sucesión de éstos en orden ascendente o descendente. Pero si en el caso de los egipcios el sistema tenía una base 10 -decenas, centenas, millares...- en el de los romanos se eligió una base mas pequeña: el 5 (los dedos de una mano). En un principio, los romanos no conocían limitación para repetir los símbolos de modo que cuatro se escribía IIII y cuarenta XXXX. De esta forma, 1999 sería MDCCCCLXXXXVIIII. Pero en una segunda fase de evolución se pensó en simplificar la numeraci6n evitando la repetición de un símbolo más de tres veces y haciendo que la posición del mismo determinara si se añadía o se restaba al siguiente. Así 1999 quedó reducido a un mucho más sencillo MCMXCIX.

En cualquier caso este sistema, igual que otros muchos que utilizaron el alfabeto escrito para la representación de números, sufría serias limitaciones. Cada vez que se superaba una determinada cantidad había que inventar un nuevo símbolo, añadir una nueva letra del alfabeto. Y éstas son muy escasas. La solución a este problema la ofreció un desconocido matemático hindú que inventó el sistema de numeración que hoy rige en la mayor parte del planeta. Hace aproximadamente 2.200 años, los hindúes manejaban los símbolos actuales: 1 para el uno, 2 para el dos, 3 para el tres... hasta el 9. A partir del 9, utilizaban símbolos distintos para el diez, el cien o el mil.

 En busca de lo simple
Hasta que, no se sabe bien cómo ni cuando, a alguien se le ocurrió una genial idea: sustituir este sistema por uno que tuviera en cuenta que el número 200 equivale a 2 veces 100, el veinte a 2 veces 10 y el 2 a un par de unos. Es decir, todas las cantidades se pueden construir con repeticiones de algo. De ese modo se creó un método en el que el primer símbolo representara el número de unos (unidad), el siguiente por la izquierda el número de dieces (decena), el siguiente el número de cientos (centena)... Así 1999 es la representación de una cantidad compuesta por 9 unidades, 9 decenas, 9 centenas y un millar. Es decir 1999 = (9 x 1 ) + (9 x 10) + (9 x 100)+(1 x 1.000).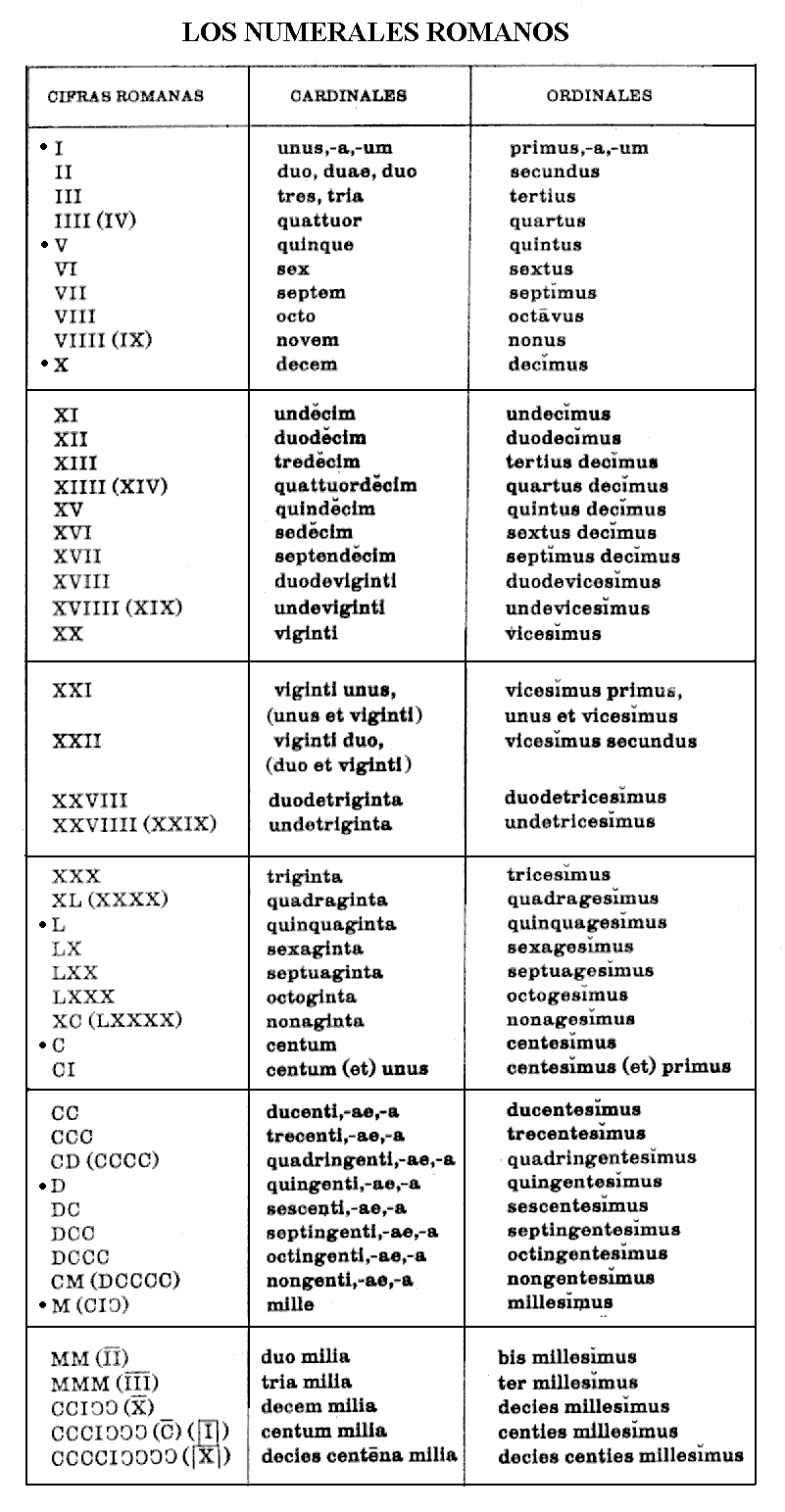

Con esta solución se resuelve el problema de los números grandes, ya que basta con ir añadiendo cifras a la izquierda para aumentar la cantidad hasta el infinito. Sin embargo, seguía habiendo una limitación. Supongamos que queremos escribir la cantidad dos mil cinco. Ésta está formada por cinco unidades y dos millares, sin centenas ni decenas. Podría representarse 25, pero llevaría a engaños. También podría dejarse un espacio intermedio 2--5 pero la tipografía de la época no permitía tales florituras sin que se produjesen errores. Había que buscar un símbolo que dejase claro que en ciertas posiciones no hay nada. La representación numérica de la nada es uno de los avances más importantes de la civilización humana y se produjo hace unos 1.300 años. También fueron los hindúes sus responsables. Había surgido el cero, con el que se podría representar cualquier cantidad grande o pequeña sin riesgo de error. Incluso el esquivo 2.005.
El original sistema de numeración hindú se extendió como la pólvora por medio mundo ya que permitía operar con grandes cifras de un modo muy sencillo. Entre los griegos y romanos, por ejemplo, realizar una división o una multiplicación medianamente complicadas requería años y años de estudios de matemáticas. Con el hallazgo de los hindúes, cualquier niño puede aprender en el colegio las reglas básicas de la aritmética. Alrededor del año 800 de nuestra era, los numerales hindúes se habían difundido por las regiones del norte de la India, donde habitaban pueblos de lengua árabe. Fue a través de la dominación islámica como llegaron estos números a España desde donde se irradió su influencia por toda Europa. En el ano 967 un francés llamado Gerberto se trasladó a la España árabe para conocer más de cerca el portentoso método de numeración del que había oído hablar. Su obra fue definitiva para que en todo Occidente se conocieran los nuevos números que por error, se llamaron números arábigos, cuando son hindúes.

Sin embargo, hubieron de pasar dos siglos más para que esta numeración se instaurara definitivamente entre los matemáticos europeos demasiado acostumbrados a trabajar con cifras romanas. El italiano Leonardo Fibonacci entró en contacto con los números hindúes durante un viaje al norte de África en 1202. Sus tratados fueron divulgados por los comerciantes, que enseguida entendieron las excelencias del nuevo sistema para llevar su contabilidad. Aun así, la impronta dejada por los romanos fue muy difícil de borrar. De hecho hoy escribimos los siglos o destacamos la importancia de papas y reyes utilizando los números legados por Roma: Juan Pablo II, siglo XX, etc...